Matteo Ruggiero's home page

Holomorphic dynamical systems

Course - 2018-2019 (1st semester) - Beijing University and BICMR. The first 12 lessons are for 4th year Maths. The last 4 lessons are for graduate-Phd students.

All classes will take place in Room 9, Quan Zhai, BICMR (see link).

Time schedule

2018.09.04: Tuesday 15h00-18h00 - room 9 Qyan Zhai, BICMR
2018.09.11: Tuesday 15h00-18h00 - room 29 Qyan Zhai, BICMR
From 2018.09.17 to 2018.11.18: Fridays 14h00-17h00 - room 9 Qyan Zhai, BICMR
From 2018.11.19: Tuesdays 09h00-12h00 - room 9 Qyan Zhai, BICMR

Period and variations to the time schedule

From 2018.09.04 to 2018.12.28
National Holiday 2018.10.01-07 : no class
The class of 2018.10.12 will not take place : it is moved to 2018.10.16 09h00-12h00 room 9 Qyan Zhai
The class of 2018.11.02 is moved to 2018.11.06 09h00-12h00 room 9 Qyan Zhai
The class of 2018.11.09 is moved to 2018.11.13 09h00-12h00 room 9 Qyan Zhai

Suggested references

Milnor - Dynamics in one complex variable (3rd edition, 2006).
Beardon - Iteration of rational functions (2000).
Carleson, Gamelin - Complex dynamics (1993).

Personal handwritten notes of the classes

Be careful, there could be mistakes, and it could differ from the given classes.

Class 01, 2018.09.04: 01 - Introduction. pdf
Class 01, 2018.09.04: 02a - Holomorphic functions. pdf
Class 02, 2018.09.11: 02b - Riemann surfaces and coverings. pdf
Class 03, 2018.09.21: 02c - Poincaré metric. pdf
Class 04, 2018.09.28: 03a - Local uniform convergence. pdf
Class 04, 2018.09.28: 03b - Normal families. pdf
Class 05, 2018.10.16: 04 - Fatou and Julia sets. pdf
Class 06, 2019.10.19: 05a - Dynamics on hyperbolic surfaces. pdf
Class 06-07, 2019.10.19-26: 05b - Tori and Lattes maps. pdf
Class 07, 2019.10.26: 06a - Contracting and repelling germs. pdf
Class 08, 2019.11.06: 06b - Tangent to the identity germs, formal classification and flower theorem. pdf
Class 09, 2019.11.13: 06c - Parabolic germs, topological and analytical classification. pdf
Class 09, 2019.11.13: 06d - Irrational germs, first results. pdf
Class 10, 2019.11.16: 06e - Diophantine conditions. pdf
Class 10, 2019.11.16: 06f - Irrational germs, linearizability and small cycles. pdf
Class 11, 2018.11.20: 07a - From local to global, attracting case. pdf
Class 11, 2018.11.20: 07b - From local to global, superattracting case. pdf
Class 12, 2018.11.27: 07c - From local to global, indifferent case. pdf
Class 12, 2018.11.27: 08a - Non-repelling vs repelling cycles. pdf
Class 13, 2018.12.04: 08b - Invariant Fatou components. pdf
Class 13, 2018.12.04: 09 - Quasiconformal surgery. pdf
Class 13, 2018.12.04: 10a - Sullivan theorem, Baker's argument. pdf
Class 14, 2018.12.11: 10b - Sullivan theorem, quasiconformal deformations. pdf
Class 14, 2018.12.11: 10c - Other applications of quasiconformal surgery. pdf
Class 15, 2018.12.18: 11 - Potential theory. pdf
Class 16, 2018.12.25: 12 - Holomorphic families of rational maps. pdf

Some images

	Filled Julia set of f(z)=z^2-0.123+0.745i (Douady's rabbit).		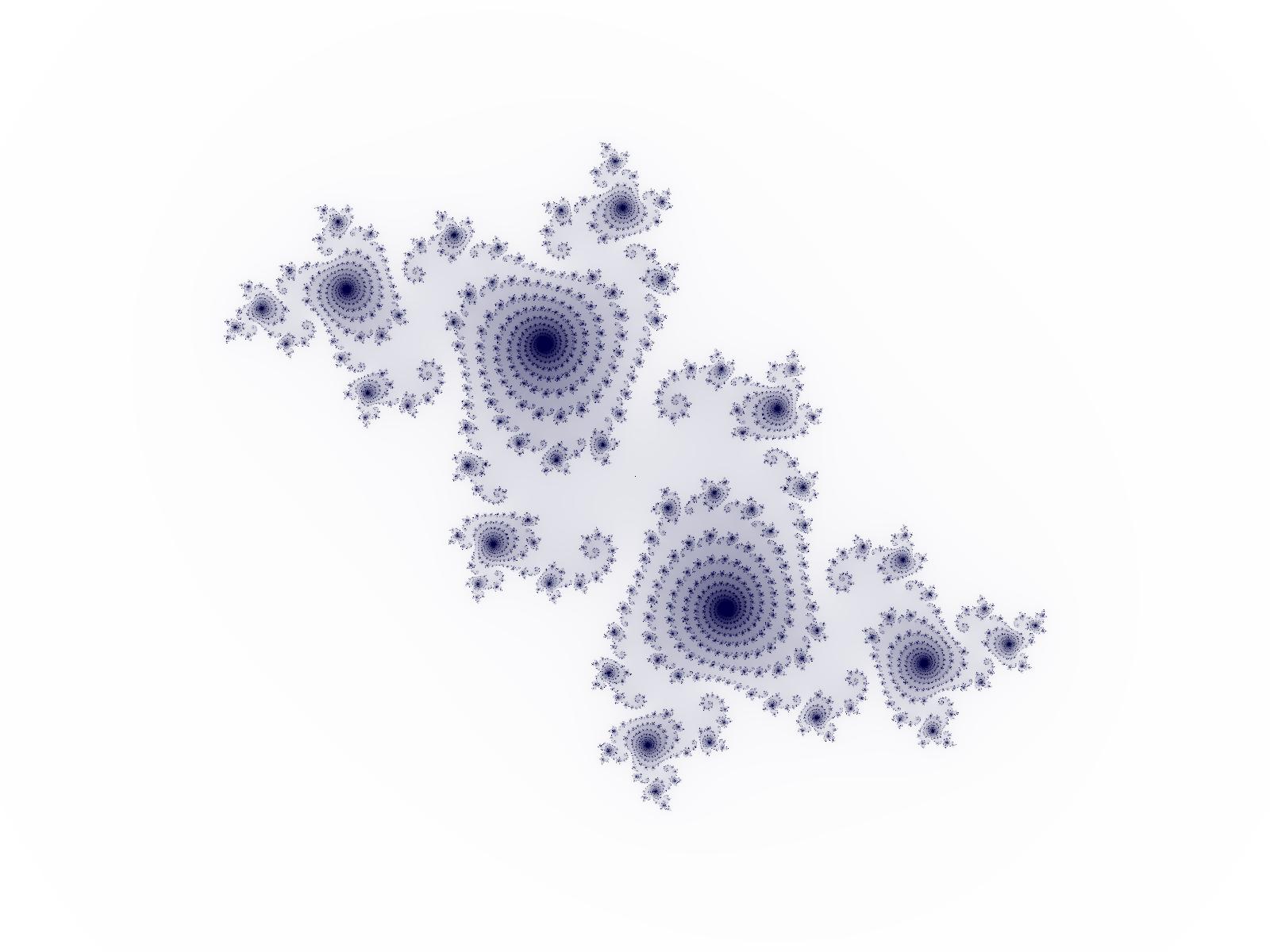Julia set of f(z)=z^2-0.194+0.6557i.
	Filled Julia set of f(z)=z^3-0.48z+0.706260+0.502896i (Douady's family of rabbits).		Julia set of f(z)=z3-0.75z+0.25isqrt10.
	Mandelbrot set (in black), associated to the family of maps f_c(z)=z^2+c.		Julia set and basins of attraction of the Newton method associated to g(z)=z^3-1.